Question

Consider function f below.


`f(x)=4^(x) -6`

Determine function g which is created by shifting the graph of function f up 5 units.

A. g(x) = 4(x + 5) - 6
B. g(x) = 9x - 6
C. g(x) = 4x - 1
D. g(x) = 4x + 5

Answer 1

Option C -
`g(x)=4^(x) -1`

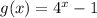
Explanation:

Given : Function
`f(x)=4^(x) -6`

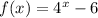
To find : Determine function g which is created by shifting the graph of function f up 5 units?

Solution :

Shifting the graph upward in the function by some unit is defined as

f(x) → f(x)+b i.e. shifting upward by b unit.

Applying the transformation rule in the given function,

`f(x)=4^(x) -6`

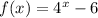
Shifting upward by 5 unit i.e. f(x)+5

`g(x)=4^(x) -6+5`

`g(x)=4^(x) -1`

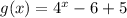
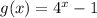
Therefore, The required function g is defined as
`g(x)=4^(x) -1` .

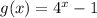So, Option C is correct.

Answer 2

For this case we have a function of the form:

`f (x) = 4 ^ x-6`

We want to move the graph five units up.

Therefore, the new function is given by:

`g (x) = f (x) +5`

Substituting we have:

`g (x) = 4 ^ x-6 + 5`

Rewriting the function:

`g (x) = 4 ^ x-1`

Answer:

The new function is given by:

`g (x) = 4 ^ x-1`

option C