Answer:
The functions
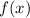 ,
,
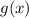 and
and
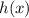 such that
such that
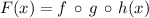 are
are
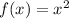 ,
,
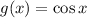 and
and
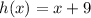 , respectively.
, respectively.
Explanation:
Let
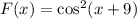 , if
, if
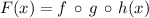 , then we derive
, then we derive
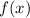 ,
,
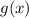 and
and
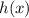 by using the following approach:
by using the following approach:
1)
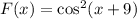 Given
Given
2)
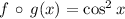 Definition of function composition/
Definition of function composition/
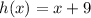
3)
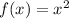 Definition of function composition/
Definition of function composition/
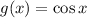
4)
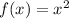 ,
,
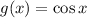 ,
,
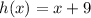 From 2) and 3)/Result
From 2) and 3)/Result
The functions
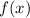 ,
,
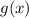 and
and
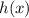 such that
such that
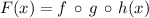 are
are
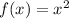 ,
,
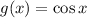 and
and
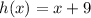 , respectively.
, respectively.