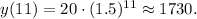Question

A population of insects grows exponentially, as shown in the table. Suppose the increase in population continues at the same rate. What is the insect population at the end of week 11? Round to the nearest whole number. Enter your answer in the box. At the end of the week 0 1 2 Insect population 20 30 45

Answer 1

`y=20\cdot (1.5)^x;`

`y(11)=1730.`

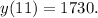
Explanation:

If a population of insects grows exponentially, then the equation
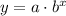`y=a\cdot b^x` represents this situation, where x is the number of weeks and y is the population.

When x=0, y=10, then
`20=a\cdot b^0=a.`

When x=1, y=30, then

`30=20\cdot b^1,\ b=(3)/(2)=1.5`

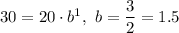
When x=2, y=45, then

`20\cdot (1.5)^2=20\cdot 2.25=45.`

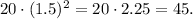
The function that represents situation is
`y=20\cdot (1.5)^x.`

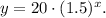
Now find y when x=11:

`y(11)=20\cdot (1.5)^(11)\approx 1730.`