Answer:
Explanation:
Graham received i penny on the first day of the month, and each day after that he received triple the number of pennies.
The sequence formed for each day pennies received will be
1, 3, 3², 3³................... n terms
Since explicit formula of a geometric series is represented by
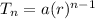
Here a = first term of the sequence = 1
r = common ratio of the sequence = 3
Now we have to calculate on which day Graham will receive 3 million dollar
So we have to find the nth term of this sequence which is equal to $3000000
Now we put these values in the explicit formula
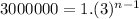
Taking log on both the sides
log(3000000) =
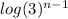
6.4771 = (n - 1)log3
6.4771 = (n - 1)(0.4771)
(n -1) =
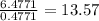
n = 13.57 + 1
n = 14.57
Therefore, on 15 the day he will get over 3 million dollars.