Answer:
95% confidence interval for the mean ARSMA score for first-generation Mexican Americans
(2.13264 , 2.58736)
Explanation:
Step(i):-
Mean of the Population = 3.0
Standard deviation of the Population = 0.8
Given Mean of the sample(x⁻ ) = 2.36
Standard deviation of the sample (S) = 0.8
size of the sample = 50
Level of significance =0.05
Degrees of freedom = n-1 = 50-1 = 49
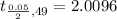
Step(ii):-
95% confidence interval for the mean ARSMA score for first-generation Mexican Americans
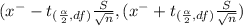
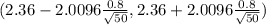
( 2.36 - 0.22736 , 2.36 + 0.22736)
(2.13264 , 2.58736)
Final answer:-
95% confidence interval for the mean ARSMA score for first-generation Mexican Americans
(2.13264 , 2.58736)