Question

A train that has wheels with a diameter of 91.44 cm (36 inches used for 100 ton capacity cars) slows down from 82.5 km/h to 32.5 km/h as the train approaches a town. The wheels of the train make 95.0 revolutions in this time.

Required:
a. What is the angular acceleration of the wheels?
b. How long does it take the train to make this reduction in speed?
c. How far does the train travel during this deceleration period?
d. Assuming the same rate of deceleration, how many MORE revolutions will the wheels make before stopping?
e. Assuming the same rate of deceleration, how much FARTHER will the train travel before stopping?

Answer 1

The answer is below

Step-by-step explanation:

The initial velocity = u = 82.5 km/h = 22.92 m/s, the final velocity = 32.5 km/h = 9.03 m/s, diameter = 91.55 cm = 0.9144 cm

radius (r) = diameter / 2 = 0.9144 / 2= 0.4572 m

a) Initial angular velocity (
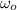`\omega_o`) = u /r = 22.92 / 0.4572 = 50.13 rad/s, final velocity (ω) = v / r = 9.03 / 0.4592 = 19.67 rad / s

θ = 95 rev * 2πr = 95 * 2π * 0.4572= 272.9 rad

angular acceleration (α) is:

`\omega^2=\omega_o^2+2\alpha \theta\\\\19.67^2-50.13^2=2\alpha(272.9)\\\\19.67^2=50.13^2+2\alpha(272.9)\\\\2\alpha(272.9)=-2126.108\\\\\alpha=-3.89\ rad/s^2\\\\`

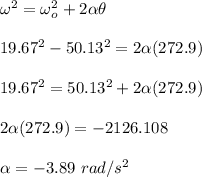
b)

`\omega=\omega_o+\alpha t\\\\19.67=50.13+(-3.89t)\\\\3.89t=50.13-19..67\\\\3.89t=30.46\\\\t=7.83\ s`

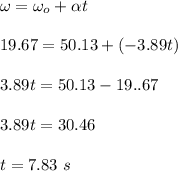
c) θ = 95 rev * 2πr = 95 * 2π * 0.4572= 272.9 rad

a) When it stops, the final angular velocity is 0. Hence:

`\omega^2=\omega_o^2+2\alpha \theta\\\\0=50.13^2+2(-3.89)\theta\\\\2(3.89)\theta=50.13^2\\\\2(3.89)\theta=2513\\\\\theta=323\ rad\\\\revolutions=(\theta)/(2\pi r)=(323)/(2\pi(0.4572)) =112.4\ rev`

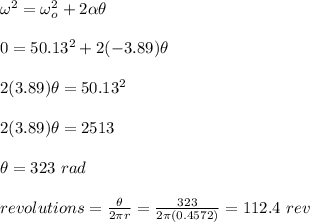
θ = 323 rad