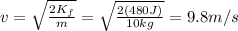Question

A 98.0 N grocery cart is pushed 12.0 m along an aisle by a shopper who exerts a constant horizontal force of 40.0 N. If all frictional forces are neglected and the cart starts from rest, what is the grocery cart's final speed?

Answer 1

9.8 m/s

Step-by-step explanation:

The work done by the force pushing the cart is equal to the kinetic energy gained by the cart:

`W=K_f -K_i`

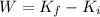
where

W is the work done

`K_f` is the final kinetic energy of the cart

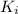`K_i` is the initial kinetic energy of the cart, which is zero because the cart starts from rest, so we can write:

`W=K_f`

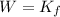
But the work is equal to the product between the pushing force F and the displacement, so

`W=Fd=(40.0 N)(12.0 m)=480 J`

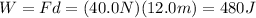
So, the final kinetic energy of the cart is 480 J. The formula for the kinetic energy is

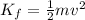`K_f=(1)/(2)mv^2` (1)

where m is the mass of the cart and v its final speed.

We can find the mass because we know the weight of the cart, 98.0 N:

`m=(F_g)/(g)=(98.0 N)/(9.8 m/s^2)=10 kg`

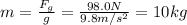
Therefore, we can now re-arrange eq.(1) to find the final speed of the cart:

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(480 J))/(10 kg)}=9.8 m/s`