Answer:
Alright, lets get started.
Please have a look at the diagram I have attached.
There are 4 vertices means A (12,2) , B (12,13), C (15,13) & D (15,2)
So, the side AB =
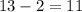
side BC =
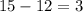
side CD =
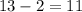
side DA =
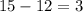
So the perimeter =
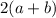
Perimeter =
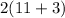
Perimeter =

Area=

Area =
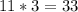
So the perimeter is 28 and area is 33. : Answer
Hope it will help :)