Question

In triangle KLM, if K is congruent to L, KL = 9x - 40, LM = 7x - 37, & KM = 3x + 23, find x & the measure of each angle.

Answer 1

Answer: x = 15, ∠K = 45.7°, ∠L = 45.7°, ∠M = 88.6°

Explanation:

Since ∠K ≅ ∠L, then ΔKLM is an isoceles triangle with base KL

KM ≅ LM

3x + 23 = 7x - 37

23 = 4x - 37

60 = 4x

15 = x

KM = LM = 3x + 23

= 3(15) + 23

= 45 + 23

= 68

KL = 9x - 40

= 9(15) - 40

= 135 - 40

= 95

Next, draw a perpendicular bisector KN from K to KL. Thus, N is the midpoint of KL and ΔMNL is a right triangle.

• Since N is the midpoint of KL and KL = 95, then NL = 47.5
• Since ∠N is 90°, then NL is adjacent to ∠l and ML is the hypotenuse

Use trig to solve for ∠L (which equals ∠K):

cos ∠L =
`(adjacent)/(hypotenuse)`

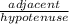
cos ∠L =
`(47.5)/(68)`

∠L = cos⁻¹
`((47.5)/(68))`

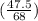
∠L = 45.7

Triangle sum Theorem:

∠K + ∠L + ∠M = 180°

45.7 + 45.7 + ∠M = 180

91.4 + ∠M = 180

∠M = 88.6