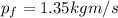Question

A ball with a mass of 0.50 kilograms is moving at a speed of 1.8 meters/second along the positive x-axis. It collides with another ball of the same mass travelling at a speed of 2.0 meters/second toward the positive y-axis. Both balls then start moving together. What is the magnitude of the resultant momentum before collision?

Answer 1

A. 1.3 kilogram meters/second

Answer 2

Answer: 1.35 kg m/s

Step-by-step explanation:

The law of conservation of momentum states that the total momentum before and after the collision is conserved, therefore:

`p_i=p_f`

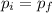
we can calculate the total momentum before the collision,
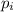`p_i`, since we know the masses and the initial velocities of the two balls.

The momentum along the x-axis is given only by the first ball, since the second one is moving on the y-axis:

`p_x = m v_1 = (0.50 kg)(1.8 m/s)=0.9 kg m/s`

The momentum along the y-axis is given only by the second ball, since the first one is moving on the x-axis:

`p_y = m v_2 = (0.50 kg)(2.0 m/s)=1.0 kg m/s`

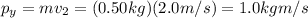
So, the magnitude of the resultant momentum is

`p_i=√(p_x^2 +p_y^2)=√((0.9 kg m/s)^2+(1.0 kg m/s)^2)=1.35 kg m/s`

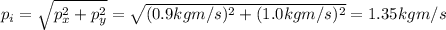
And since the total momentum after the collision is equal to the momentum before the collision,

`p_f = 1.35 kg m/s`