Answer:
Route y= 31 miles.
Route x= 24 miles.
Explanation:
We have been given that each week Dan drives two routes: route x and route y.
One week he drives route x three times and route y 2 times. He drives a total of 134 miles that week. We can represent this information as:
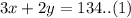
Another week he drives route x twice and route y 5 times. He drives a total of 203 miles.We can represent this information as:
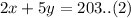
Upon using our given information we have formed a system of equations. Now we will solve our system of equations using substitution method.
From equation 1 we will get,
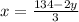
Upon substituting this value in 2nd equation we will get,
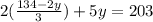
Upon distributing 2 we will get,
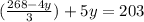
Now we will find a common denominator for left side of our equation.
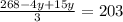

Upon multiplying both sides of our equation by 3 we will get,
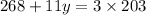
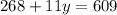
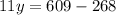

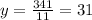
Therefore, the length of route y is 31 miles.
Now let us substitute y=31 in 1st equation to find the value of x.


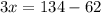
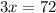
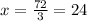
Therefore, the length of route x is 24 miles.