Question

(cosxtanx-tanx+2cosx-2)/tanx+2=cosx-1
can someone show me how to prove this?

Answer 1

See detail below.

Explanation:

A word of caution before getting to the actual problem: I believe there is an important set of brackets missing in the original post. The expression on the left hand side should be:

(cosxtanx-tanx+2cosx-2)/(tanx+2)

Without the brackets, it is left unclear whether the denominator is just tanx or tanx+2. I recommend to use brackets wherever any doubt could arise.

Now to the actual problem: \we can make the following transformations on the left hand side:

`(\cos x \tan x + 2\cos x -2)/(\tan x +2)=(\cos x (\sin x)/(\cos x)  + 2\cos x -2)/((\sin x +2\sin x)/(\cos x) )=\\=(\cos x \sin x - \sin x + 2\cos^2 x - 2\cos x)/(\sin x + 2\cos x)=\\=(\cos x \sin x +2\cos^2 x )/(\sin x + 2\cos x)-1=\\=\cos x -1`

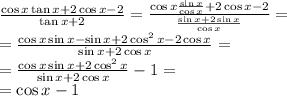
which is shown to be the same as the right hand side, which was to be shown.