Question

A marble is dropped off the top of a building. Find it's velocity and how far below to its dropping point for the first 10 seconds of the drop .Use g=-9.8m/s^2

Answer 1

1) velocity: 98 m/s downward

Step-by-step explanation:

The marble moves by uniformly accelerated motion, with constant acceleration a=g=-9.8 m/s^2 directed towards the ground. Therefore, its velocity at time t is given by:

`v(t)=v_0 +at`

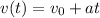
where

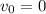`v_0 = 0` is the initial velocity

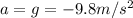`a=g=-9.8 m/s^2` is the acceleration

`t` is the time

Substituting t = 10 s, we find:

`v(10 s)=0+(-9.8 m/s^2)(10 s)=-98 m/s`

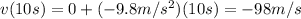
And the negative sign means the direction of the velocity is downward.

2) Distance covered: 490 m

The distance covered in an uniformly accelerated motion can be found with the formula:

`S=(1)/(2)at^2`

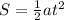
where

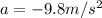`a=-9.8 m/s^2` is the acceleration

t is the time

Substituting t=10 s, we find

`S=(1)/(2)at^2=(1)/(2)(-9.8 m/s^2)(10 s)^2=-490 m`

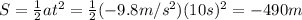
And the negative sign means the displacement is below the dropping point.