Answer:
The rational numbers are
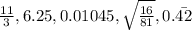 and the irrational functions are
and the irrational functions are
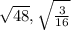 .
.
Explanation:
A rational number can be expressed in the form of
 , where p and q are integers and q is not equal to 0. For example
, where p and q are integers and q is not equal to 0. For example
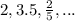 .
.
An irrational function can not be expressed in the form of
 , where p and q are integers and q is not equal to 0. For example
, where p and q are integers and q is not equal to 0. For example
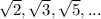 .
.
If any number is multiplied by a irrational number then the resultant number is an irrational number.
By the above definition we can conclude that:
The number
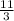 is a rational number.
is a rational number.
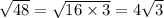
Therefore
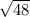 is an irrational number.
is an irrational number.
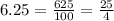
Therefore 6.25 is a rational number.
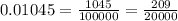
Therefore 0.01045 is a rational number.
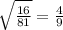
The number
 is a rational number.
is a rational number.
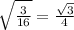
The number
 is an irrational number.
is an irrational number.
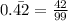
Therefore
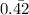 is an irrational number. The numbers with recursive bar are always rational numbers.
is an irrational number. The numbers with recursive bar are always rational numbers.