Answer: Probability that a plant grows at a constant rate, given it is edible is given by
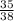 .
.
Explanation:
Let B be an event that getting a plant grows at a constant rate.
Since we have given that
The probability that a plant is edible is given by

The probability that a plant grows at a constant rate and is edible is given by
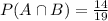
We will use "Conditional probability ", i.e.
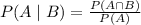
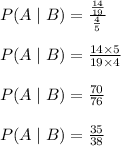
Hence, Probability that a plant grows at a constant rate, given it is edible is given by
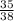 .
.