Answer:
Option C
Explanation:
Given expression is
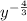 .
.
Exponent of this expression is
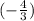 .
.
Option (A)
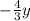
Since, exponents and coefficients of both the expressions are different.
They are not equivalent.
Option (B)
![-(\sqrt[3]{y})^4=-(y^{(1)/(3)})^4](https://img.qammunity.org/2022/formulas/mathematics/high-school/azx66yghzb5xtgduuevcpecw7y0b17t1ew.png)
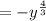
Here, exponent is with positive notation
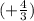 while in the original expression it is negative
while in the original expression it is negative
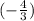 .
.
Therefore, both the expressions are not equivalent.
Option (C)
![\frac{1}{(\sqrt[3]{y})^4}=(\sqrt[3]{y})^(-4)](https://img.qammunity.org/2022/formulas/mathematics/high-school/bkitso5am51eoeovhsbyjgu3xm8l21v9wq.png)
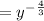
Both the expressions are equivalent.
Option (D)
![-(\sqrt[4]{y})^3=-(y)^{(3)/(4)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/xysnkz1v2xzymqjuy97alcnmpfvwnmx3sz.png)
Exponents of both the expressions are different.
Therefore, not equivalent.
Option (E)
![\frac{1}{(\sqrt[4]{x})^3}=(\sqrt[4]{x})^(-3)](https://img.qammunity.org/2022/formulas/mathematics/high-school/bo3h8ptkewfpxqszne0sfup5ixg07t2f95.png)
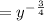
Exponent of this expression is different from the original expression.
Therefore, not equivalent.
Option (C) will be the correct option.