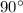Question

If two consecutive angles of a parallelogram are congruent, what is the measure of each angle?

Answer 1

Measure of each angle is 90 degree.

Explanation:

Given : If two consecutive angles of a parallelogram are congruent.

To find the measure of each angle:

There are 6 important properties of parallelograms:

• Opposite sides are congruent.

• Opposite angles are congruent
• Consecutive angles are supplementary.
• If one of the angle is right angle, then all angles are right.
• Diagonals of a parallelogram bisect each other
• Also, each diagonal of a parallelogram separates it into two congruent.

let A and D be two consecutive angle.

then, by the given condition

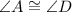`\angle A \cong \angle D` ......[1]

From the property of parallelogram:

Consecutive angles are supplementary

Then;

`\angle A + \angle D = 180^(\circ)`

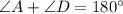
From equation [1];

`\angle A + \angle A = 180^(\circ)`

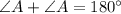
Combine like terms :

`2\angle A = 180^(\circ)`

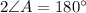
Divide both sides by 2 we get;

`(2 \angle A)/(2) = (180^(\circ))/(2)`

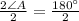
Simplify:

`\angle A = 90^(\circ)`

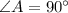
From the given property of parallelogram : if one of the angle is right, then all the angles in the parallelogram are right angle.

∴
`\angle A = \angle B = \angle C = \angle D = 90^(\circ)`

Therefore, the measure of each angle is
`90^(\circ)`