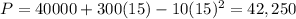Question

There are 50 apple trees in an orchard. Each tree produces 800 apples. For each additional tree planted in the orchard, the output per tree drops by 10 apples. This is represented by p=40,000+300x-10x^2, where P stands for the total production of apples and x stands for the number of trees added.

a. What is the maximum number of trees that should be added to get the maximum amount of production?

b. What is the maximum production of apples?

Answer 1

1. 15
2. 42,250

Explanation:

The given function is,

`P=40000+300x-10x^2`

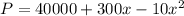
where,

P = the total production of apples,

x = the number of trees added.

As the quadratic function has a negative leading coefficient, so it will open downward and at the vertex the value of function is maximum.

The vertex will be at
`\left(-(b)/(2a),-f\left((b)/(2a)\right )\right)`

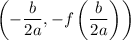
The value of the function will be maximum at,

`x=-(b)/(2a)`

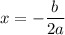
Putting the values,

`x=-(300)/(2* (-10))=(300)/(2* 10)=(300)/(20)=15`

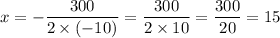
So at x=15 or for 15 number of trees the production will be ,maximum.

Putting x=15 in f(x) will yield the maximum production of apples.

`P=40000+300(15)-10(15)^2=42,250`