Question

Which answer describes the type of sequence?

1/6, 1/2, 3/2, 9/2, ...


neither arithmetic nor geometric

geometric

arithmetic

Answer 1

The sequence is a geometric sequence.

Explanation:

The given sequence is

`(1)/(6),(1)/(2),(3)/(2),(9)/(2),...`

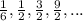
We examine to see whether there is a common difference or a common ratio.

We first check for a common difference by subtracting the subsequent terms.

`(1)/(2)-(1)/(6)=(2)/(3)`

`(3)/(2)-(1)/(2)=1`

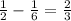
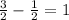
The two differences are not equal.

Hence the sequence is not arithmetic.

We now look out for a common ratio.

`(1)/(2)/ (1)/(6)=3`

`(3)/(2)/ (1)/(2)=3`

`(9)/(2)/ (3)/(2)=3`

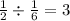
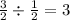
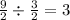
Since there is a common ratio of 3, the sequence is geometric.