Answer:
The composite function is
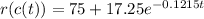 .
.
Explanation:
It is given that the effect of caffeine, c, in milligrams, on a person’s heart rate, r, in beats per minute can be modeled by the function
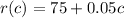 .... (1)
.... (1)
The dissipation of caffeine from the bloodstream over time since ingestion, t, in hours can be modeled by the function
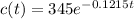 .... (2)
.... (2)
We have to find the composite function r(c(t)).
Using equation (1), we get
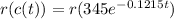
Using equation (2), we get

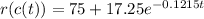
Therefore the composite function is
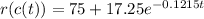 .
.