Answer:
The given function is a nonlinear function because the degree of the function is 2 and we get same value of y for more than one values of x.
Explanation:
The given function is
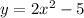
To find the points which lie on the function, put difference values of x in the given function and find the values of y.
Put x= -2
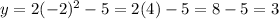
Put x= -1
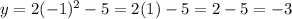
Put x= 0
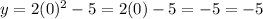
Put x=1
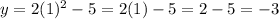
Put x= 2
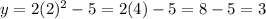
The table of values is shown below.
Plot these points on a coordinate plane and connect them by a free hand curve.
The given function is a nonlinear function because the degree of the function is 2 and we get same value of y for more than one values of x.
The graph of function is shown below.