Question

Final exam scores are normally distributed with a mean of 74 and a standard deviation of 6. Approximately, what percentage of final exam scores would be between 68 and 86?

Answer 1

81.86%

Explanation:

We have been given that final exam scores are normally distributed with a mean of 74 and a standard deviation of 6.

First of all we will find z-score using z-score formula.

`z=(x-\mu)/(\sigma)`

`z=(68-74)/(6)`

`z=(-6)/(6)=-1`

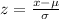
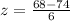
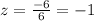
Now let us find z-score for 86.

`z=(86-74)/(6)`

`z=(12)/(6)=2`

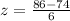
Now we will find P(-1<Z) which is probability that a random score would be greater than 68. We will find P(2>Z) which is probability that a random score would be less than 86.

Using normal distribution table we will get,

`P(-1<Z)= .15866`

`P(2>Z)=.97725`

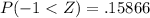
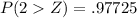
We will use formula
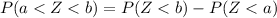`P(a<Z<b) = P(Z<b) - P(Z<a)` to find the probability to find that a normal variable lies between two values.

Upon substituting our given values in above formula we will get,

`P(-1<Z<2) = P(Z<2) - P(Z<-1)`

`P(-1<Z<2) = 0.97725-0.15866=0.81859`

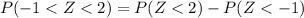
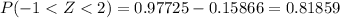
Upon converting 0.81859 to percentage we will get

`0.81859*100=81.859\approx 81.86`

Therefore, 81.86% of final exam score will be between 68 and 86.