Question

Heather drives her Super-Beetle around a turn on a circular track which has a radius of 200 m. The Super-Beetle has a mass of 1500 kg and the coefficient of static friction between the road and tires is 0.6.

a. What is the force of static friction the road can apply batore the car starts to selon (use Ft= uFn).
b. What is the maximum speed the car can travel before it would start to slide?

Answer 1

The force of static friction that can be applied before the car starts to slide is 8829 N. The maximum speed the car can travel on the curve without sliding is approximately 17.15 m/s.

Step-by-step explanation:

Force of Static Friction and Maximum Car Speed on a Curve

To determine the force of static friction (a) that can be applied before the car starts to slide, we can use the equation Ft = μFn, where Ft is the force of static friction, μ is the coefficient of static friction, and Fn is the normal force. For a car on level ground, the normal force is equal to its weight, so Fn = mg, where m is the mass of the car and g is the acceleration due to gravity. Using this, we find that Ft = (0.6)(1500 kg)(9.81 m/s²) which equals 8829 N.

As for the maximum speed (b) the car can travel without sliding, we use the relationship Fc = mv²/r, where Fc is the centripetal force needed to keep the car moving in a circle, v is the speed, and r is the radius of the circular track. Setting the centripetal force equal to the maximum force of static friction, we get 8829 N = (1500 kg)v²/(200 m). Solving for v gives us a maximum speed of approximately 17.15 m/s.

Answer 2

a) The force of static friction the road can apply before the car starts to move is 8826.3 newtons.

b) The maximum speed that a car can travel before it would start to slide is approximately 34.305 meters per second.

Step-by-step explanation:

a) Let suppose that the car is on a horizontal ground and travels at constant speed. The vehicle experiments a centripetal acceleration due to friction, which can be seen in the Free Body Diagram (please see image attached for further details). By Newton's Laws, we construct the following equations of equilibrium:

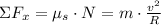`\Sigma F_(x) = \mu_(s)\cdot N = m\cdot (v^(2))/(R)` (1)

`\Sigma F_(y) = N -m\cdot g = 0` (2)

Where:

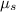`\mu_(s)` - Static coefficient of friction, dimensionless.

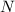`N` - Normal force from ground to the car, measured in newtons.

`v` - Maximum speed of the car, measured in meters per second.

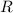`R` - Radius of the circular track, measured in meters.

`m` - Mass, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

By applying (2) in (1):

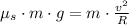`\mu_(s)\cdot m\cdot g = m\cdot (v^(2))/(R)` (3)

The force of static friction the road can apply in the car (
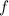`f`), measured in newtons, is: (
`\mu_(s) = 0.6`,
`m = 1500\,kg`,
`g = 9.807\,(m)/(s^(2))`)

`f = \mu_(s)\cdot m \cdot g`

`f = (0.6)\cdot (1500\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)`

`f = 8826.3\,N`

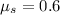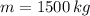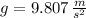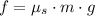
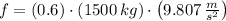
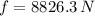
The force of static friction the road can apply before the car starts to move is 8826.3 newtons.

b) Then, we calculate the maximum speed of the car by (3):

`\mu_(s)\cdot m\cdot g = m\cdot (v^(2))/(R)`

`\mu_(s)\cdot g = (v^(2))/(R)`

`v = \sqrt{\mu_(s)\cdot g\cdot R}`

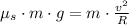
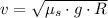
If we know that
`\mu_(s) = 0.6`,
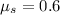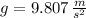`g = 9.807\,(m)/(s^(2))` and
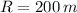`R = 200\,m`, then the maximum speed of the car can travel before it would start to slide is:

`v =\sqrt{(0.6)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (200\,m)}`

`v \approx 34.305\,(m)/(s)`

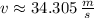
The maximum speed that a car can travel before it would start to slide is approximately 34.305 meters per second.