Question

A horizontal spring has spring constant k = 360 N/m. First, compress the spring from its uncompressed length (x = 0) to x = 11.0 cm. Second, a 1.85-kg block is placed against the spring and the spring is released, what will be the speed of the block when it separates from the spring at x = 0? Ignore friction.

Answer 1

Here we can say that by energy conservation principle

Elastic potential energy of spring will convert into kinetic energy of the block

so here we will have

`(1)/(2) kx^2 = (1)/(2)mv^2`

we also know that

k = 360 N/m

x = 11 cm

m = 1.85 kg

now we will use all in above equation

`(1)/(2)* 360* (0.11)^2 = (1)/(2)* (1.85) v^2`

`4.356 = 0.925 v^2`

`v^2 = 4.71`

`v = 2.17 m/s`

so it will move with speed 2.17 m/s after separating from spring

Answer 2

The speed of the block when it separates from the spring will be
`v=1.53(m)/(s)`

Step-by-step explanation:

Using the Principle of Conservation of Energy, and taking into account that we have a system of a spring and a block that we can analyze, we can say that in two different instants, the energy must be constant.

Now, we can think in the initial moment, when the spring is compressed and the block is against it, and write its energy as potential energy because the kinetic energy is zero as they are not moving:

`E_(i)=(1)/(2)kx^2`

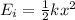
where k is the spring constant, and x is the length of compression of the spring (this length will be expressed in m instead of cm to be consistent with the units).

Then we can go to the final moment when the block is "separating" from the spring, and in that moment the potential energy will be zero, and all energy will be kinetic, wich we can write as

`E_(f)=(1)/(2)mv^2`

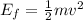
where m is the mass of the block, and v is its speed (this is what we want to calculate). Therefore, we can equalize both expressions, and clear v

`(1)/(2)kx^2=(1)/(2)mv^2\Leftrightarrow v=\sqrt{(kx^2)/(m)}\Leftrightarrow v=\sqrt{(360(0.11)^2)/(1.85)(m^2)/(s^2)}`

Finally, we have that

`v=1.53(m)/(s)`

wich is the speed of the block when it separates from the spring.