Question

What are the coordinates of the endpoints of the midsegment for △DEF that is parallel to DE¯¯¯¯¯?

Answer 1

The coordinates of the endpoints of the midsegment for △DEF are: (-1, 2) & (-1, 3.5). Hope this helps~

Answer 2

The correct answer is: (-1, 3.5) and (-1, 2)

Step-by-step explanation:

First let's find the equation of DF (for the sake of understanding, consider it a line).

Point D = (1,4)

Point F = (-3,3)

The slope of DF is:
`(y_2-y_1)/(x_2-x_1) = (3-4)/(-3-1) = (-1)/(-4) = (1)/(4)`

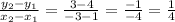
The equation of line is: y = mx + c

Where m = slope =
`(1)/(4)`

Equation for DF will become:
`y = (1)/(4)x + c`

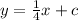
To find c, plug any point (D or F) in the above equation. I am going to choose D.

4 = (1/4) + c

c = 3.75

So the equation for DF will become: y = (1/4)x + 3.75 --- (A)

Likewise, let's find the equation for EF (again assume that it is a line).

Point E = (1,1)

Point F = (-3,3)

The slope of EF is:
`(y_2-y_1)/(x_2-x_1) = (3-1)/(-3-1) = (2)/(-4) = (-1)/(2)`

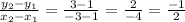
The equation of line is: y = mx + c

Where m = slope =
`(-1)/(2)`

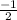
Equation for EF will become:
`y = (-1)/(2)x + c`

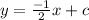
To find c, plug any point (E or F) in the above equation. I am going to choose E.

1 = (-1/2) + c

c = 1.5

So the equation for EF will become: y = (-1/2)x + 1.5 --- (B)

We can see in the graph that the midsegment that is parallel to DE will be at x = -1 (two unit to the left of DE), since the △DEF is 4 units wide.

Put x = -1 in equation (A) to get the upper endpoint of the midsegment:

y = (1/4)(-1) + 3.75

y = 3.5 (when x = -1) <-- Upper endpoint

Put x = -1 in equation (B) to get the lower endpoint of the midsegment:

y = (-1/2)(-1) + 1.5

y = 2 (when x = -1) <-- lower endpoint

Hence, (-1, 3.5) and (-1, 2) is the correct answer.