Answer:
(a) the fundamental frequency of this string is 65 Hz
(b) the harmonics of the given frequencies are third and fourth respectively.
(c) the length of the string is 2.74 m
Step-by-step explanation:
Given;
mass density of the string, μ = 3 x 10⁻³ kg/m
tension of the string, T = 380 N
resonating frequencies, 195 Hz and 260 N
For the given resonant frequencies;
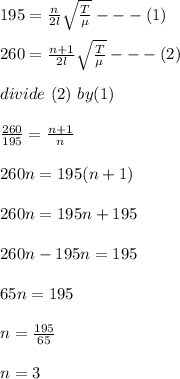
(c) From any of the equations, solve for Length of the string (L);
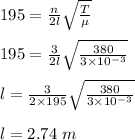
(a) the fundamental frequency is calculated as;
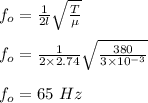
(b) harmonics of the given frequencies;
the first harmonic (n = 1) = f₀ = 65 Hz
the second harmonic (n = 2) = 2f₀ = 130 Hz
the third harmonic (n = 3) = 3f₀ = 195 Hz
the fourth harmonic (n = 4) = 4f₀ = 260 Hz
Thus, the harmonics of the given frequencies are third and fourth respectively.