Question

The graph of f(x) = x6 – 2x4 – 5x2 + 6 is shown below.

How many roots of f(x) are rational numbers?
1
2
4
6

Answer 1

B. 2

Explanation:

got it right on the quiz

Answer 2

There are two rational roots for f(x)

Explanation:

We are given a function

`f(x) = x^6-2x^4-5x^2+6`

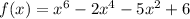
To find the number of rational roots for f(x).

Let us use remainder theorem that when

f(a) =0, (x-a) is a factor of f(x) or x=a is one solution.

Substitute 1 for x

f(1) = 1-2-5+6=0

Hence x=1 is one solution.

Let us try x=-1

f(-1) = 1-2-5+6 =0

So x =-1 is also a solution and x+1 is a factor

We can write f(x) by trial and error as

`f(x) = (x-1)(x+1)(x^2-3)`

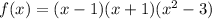
We find that
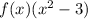`f(x) (x^2-3)` factor gives two irrational solutions as

±√3.

Hence number of rational roots are 2.