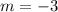1 Answer

Abderrazak BOUADMA · Answer 1 · 2019-03-02T13:29:42+0000

For this case we have that by definition, the equation of a line of slope-intercept form is given by:

y = mx + b

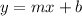
Where:

m: It is the slope, which can be found by having two points that cross the line:
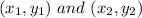$(x_ {1}, y_ {1})\ and\ (x_ {2}, y_ {2})$ .

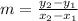
$m = \frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}$

b: It is the cut point with the y axis

If we have an equation of the form:
y = -3x + 2

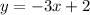
So:

$m = -3\\b = 2$

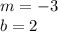
Thus, the slope of the line is
m = -3

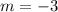
Answer:

The slope of the line is

Please log in or register to add a comment.