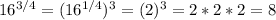Question

Please help parts b and c

Answer 1

a = 2

b = 4

c = 8

Explanation:

Remember the relationship:

`(a^(x))^(y) = a^(x*y)`

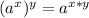
First, in "a" we have:

a)
`8^(1/3) = \sqrt[3]{8} = 2`

then in the next ones, we can use the result that we obtained in the part a:

b)
`8^(2/3) = (8^(1/3))^2 = (2)^2 = 4`

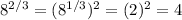
Now we can do exactly the same in c:

c) where first we need to know that:

2*2*2*2 = 4*4 = 16

then:

2^4 = 16

then:

`\sqrt[4]{16} = 16^(1/4) = 2`

Now let's solve the problem:

`16^(3/4) = (16^(1/4))^3 = (2)^3 = 2*2*2 = 8`