Question

Points (2, 0) and (0, 3) lie on line k. What is the slope of the line that is perpendicular to k? A. 3/2 B. - 3/2 C. 2/3 D. undefined

Answer 1

C: 2/3

Explanation:

Line k passes thru Points (2, 0) and (0, 3). As we move from (2,0) to (0,3), x decreases by 2 to 0 and y increases by 3 to 3. Thus, the slope of this line k is m = rise / run = -3 / 2.

Any line perpendicular to line k has a slope that is the negative reciprocal of -3/2. In other words, such a line has the slope 2/3. Answer C is correct.

Answer 2

Slope of a Line Passing through two points (x₁ , y₁) and (x₂ , y₂) is given by :

`\heartsuit\;Slope(m) = (y_1 - y_2)/(x_1 - x_2)`

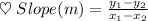
here x₁ = 2 and x₂ = 0 and y₁ = 0 and y₂ = 3

`\heartsuit\;Slope(m) = (0 - 3)/(2 - 0) = (-3)/(2)`

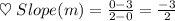
⇒ Slope of the line k is
`(-3)/(2)`

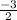
We know that : If two lines are perpendicular, then the product of slopes of the two lines should be equal to -1

⇒ Slope of line k × Slope of line perpendicular to k = -1

⇒
`(-3)/(2) * Slope\;of\;line\;perpendicular\;to\;line\;k = -1`

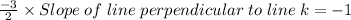
⇒ Slope of line perpendicular to line =
`(2)/(3)`

Option C is the Answer