Answer: Mean = 3.5 , median = 2.5, mode = 2, geometric mean = 2.74
Median is the most appropriate measure of central tendency.
The least appropriate = mean
Yes there is an outlier.
Step-by-step explanation:
Given responses : 5, 4, 2, 1, 1, 2, 10, 2, 3, 5.
First arrange them in increasing order,
![\sqrt[10]{1*1*2*2*2*3*4*5*5*10 }\\\\=\sqrt[10]{24000} \approx2.74](https://img.qammunity.org/2022/formulas/mathematics/college/pyrdu3nd5dc6vy64c1ttk865697alhpm5p.png)
Its sum = 35
Mean of n observations = (Sum of observations) ÷ n
Mean = (35) ÷ 10
=3.5
Here n =10 (even)
Median = average of middle most numbers =
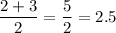
Mode = most repeated number = 2 (thrice)
geometric mean =
![\sqrt[n]{x_1* x_2*.... x_n}](https://img.qammunity.org/2022/formulas/mathematics/college/o0bn8rnjaovt1ise4p8s4es9jb7jm26x5m.png)
10 is an outlier as it is very large as compare to other numbers.
When outlier is present in data , the median is the most appropriate measure of central tendency.
Mean affected badly by the outlier so it the least appropriate.