Question

The map of a walking trail is drawn on a coordinate grid with three points of interest. The trail starts at R(−3, 2) and goes to S(2, 2) and continues to T(2, −5). The total length of the walking trail is ____ units. (Input whole numbers only.)

Answer 1

Answer:12 units

Explanation:

Point R is (-3,2) and point S is (2,2)

distance between them is

RS=
`√(5^2+0^2)`=5

ST=
`√(7^2+0^2)`=7

Total distance is RS+ST=5+7=12 units

Answer 2

Find out the the total length of the walking trail .

To prove

Formula

`Distance\ formula = \sqrt{(x_(2) - x_(1))^(2) +( y_(2) - y_(1))^(2)}`

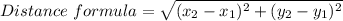
As given

The trail starts at R(−3, 2) and goes to S(2, 2) and continues to T(2, −5).

`RS = \sqrt{(2-(-3))^(2) +( 2 - 2)^(2)}`

`RS = \sqrt{( 2 - (-3))^(2)}`

`RS = \sqrt{5^(2)}`

`RS = √(25)`

`√(25) = 5`

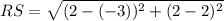
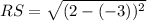
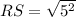
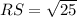
RS = 5 units

As given

S(2, 2) and continues to T(2, −5).

Now

`ST = \sqrt{(2-2)^(2) +( -5-2 )^(2)}`

`ST = \sqrt{( - 7)^(2)}`

`ST = √(49)`

`√(49) = 7`

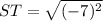
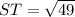
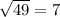
ST = 7 units

Therefore

Total length of the trail = RS + ST

= 5 units + 7 units

= 12 units

Therefore the total length of the trail is 12 units.