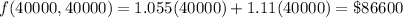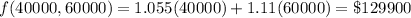Question

The Fiedler family has up to $130,000 to invest. They decide that they want to have at least $40,000 invested in stable bonds yielding 5.5% and that no more than $60,000 should be invested in more volatile bonds yielding 11%. How much should they invest in each type of bond to maximize income if the amount in the stable bond should not exceed the amount in the more volatile bond? What is the maximum income?

Answer 1

They should invest $40,000 in stable bonds and $60,000 in volatile bonds. Their maximum income is $129,900

Explanation:

Let us assume that, they invested x in stable bonds and y in volatile bonds.

The Fiedler family has up to $130,000 to invest.

`x+y\le130000`

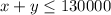
They decide that they want to have at least $40,000 invested in stable bonds.

`x\ge40000`

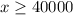
They decide that they want no more than $60,000 should be invested in more volatile bonds.

`y\le60000`

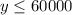
The amount in the stable bond should not exceed the amount in the more volatile bond, so

`x\le y`

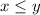
As we have to find maximum income from stable bonds yielding 5.5% and volatile bonds yielding 11%, so we have to maximize
`1.055x+1.11y`

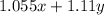
Here,

Max
`1.055x+1.11y`

`x+y\le130000`

`x\le y`

`x\ge40000`

`y\le60000`

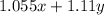
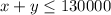
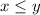
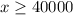
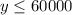
Using LPP, plotting the inequalities on graph, we get the feasible region as shown in the attachment.

The solutions to the system are,

`(40000,60000),(40000,40000),(60000,60000)`

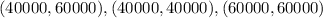
Now putting all the solutions in the objective function to find the maximize the function.

`f(40000,60000)=1.055(40000)+1.11(60000)=\$108800`

`f(40000,40000)=1.055(40000)+1.11(40000)=\$86600`

`f(40000,60000)=1.055(40000)+1.11(60000)=\$129900`