Answer:
a) The z-score for a backyard structure costing $2300 is -0.57.
b) The z-score for a backyard structure costing $4900 is 1.29
c) A backyard structure costing $2300 costs 0.57 standard deviations below the mean, while a backyard structure costing $4900 costs 1.29 standard deviations above the mean. Since both are within 2 standard deviations of the mean, none is an outlier.
d) Since this combination costs more than 2 standard deviations from the mean, yes, it should be considered an outlier.
Explanation:
Z-score:
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
If the z-score is more than two standard deviations from the mean(lesser than -2 or more than 2), the score X is considered an outlier.
In this question, we have that:
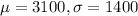
a. What is the z-score for a backyard structure costing $2300?
We have to find Z when
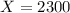 . So
. So

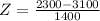

The z-score for a backyard structure costing $2300 is -0.57.
b. What is the z-score for a backyard structure costing $4900?
We have to find Z when
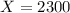 . So
. So


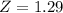
The z-score for a backyard structure costing $4900 is 1.29
c. Interpret the z-scores in parts (a) and (b). Comment on whether either should be considered an outlier.
A backyard structure costing $2300 costs 0.57 standard deviations below the mean, while a backyard structure costing $4900 costs 1.29 standard deviations above the mean. Since both are within 2 standard deviations of the mean, none is an outlier.
d. If the cost for a backyard shed-office combination built in Albany, California, is $13,000, should this structure be considered an outlier?
We have to find the z-score when X = 13000. So

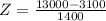
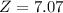
Since this combination costs more than 2 standard deviations from the mean, yes, it should be considered an outlier.