Answer:
Hence, (75,40) is the maximum point and maximum profit is $192.5
Explanation:
Let the breakfast be x
And let the lunch or afternoon be y
Inequalities will become
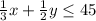
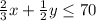
And objective function will be
Z=1.5x+2.0y
You can see the graph in the attachement
ABCD is the feasible region
Points of feasible region is (0,90) ,(0,0) ,(75,40) and(105,0)
We have to find Z by substituting the points of feasible region
At (0,90) we get
Z=1.5(0)+2(90)
Z=180
At (0,0)
Z=1.5(0)+2(0)
Z=0
At (75,40)
Z=1.5(75)+2(40)
Z=192.5
At (105,0)
Z=1.5(105)+2(0)
Z=157.5
The maximum number we are getting is 192.5 which is at (75,40)
Hence, (75,40) is the point of maximum