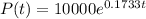Question

A petri dish has 10, 000 bacteria in it. After 4 hours the bacteria’s population increased to 20,000. If the number of colonies grows exponentially, write a formula for the number of bacteria in the dish at any time t, where t is in hours

Answer 1

`P(t) = 10000e^(0.1733t)`

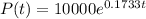
Explanation:

The population of bacteria grows exponentially, which means that it can be represented by a function in the following format:

`P(t) = P(0)e^(rt)`

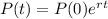
In which P(0) is the initial population and r is the growth rate.

A petri dish has 10, 000 bacteria in it.

This means that
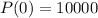`P(0) = 10000`. So

`P(t) = 10000e^(rt)`

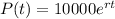
After 4 hours the bacteria’s population increased to 20,000.

This means that
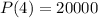`P(4) = 20000`, and we use this to find the growth rate. So

`P(t) = 10000e^(rt)`

`20000 = 10000e^(4r)`

`e^(4r) = (20000)/(10000)`

`e^(4r) = 2`

`\ln{e^(4r)} = ln(2)`

`4r = ln(2)`

`r = (ln(2))/(4)`

`r = 0.1733`

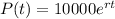
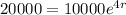
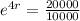
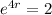
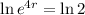
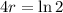
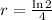
So, the formula is given by:

`P(t) = 10000e^(0.1733t)`