Question

Derive the equation of the parabola with a focus at (2, 4) and a directrix of y = 8. f(x) = −one eighth (x − 2)2 + 6 f(x) = one eighth (x − 2)2 + 6 f(x) = −one eighth (x + 2)2 + 8 f(x) = one eighth (x + 2)2 + 8

Answer 1

Answer: f(x) = −one eighth (x − 2)2 + 6

Answer 2

A

Explanation:

For any point (x, y ) on the parabola the focus and directrix are equidistant

Using the distance formula

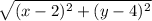`√((x-2)^2+(y-4)^2)` = | y - 8 |

Squaring both sides gives

(x - 2)² + (y - 4)² = (y - 8)²

(x - 2)² + y² - 8y + 16 = y² - 16y + 64 ( rearrange and simplify )

(x - 2)² = - 8y + 48

8y = - (x - 2)² + 48

y = -
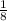`(1)/(8)`(x - 2)² + 6 → A