Question

For the data set 6,5,10,11,13, the mean, x, is 9. What is the standard deviation?

Answer 1

the answer is 3.39 but you wanna round up so 3.4 is the correct answer = 3.4

Explanation:

Answer 2

3.39

Step-by-step explanation:

We will use SD formula to find our answer.

`\sigma=\sqrt{ \frac{\sum (x-\overline{x})^(2)}{N-1} }`

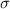`\sigma`= Standard deviation.

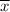`\overline{x}`= Mean.

N= Numbers of data-points.

We have been given that mean of our data set is 9. So we will find the square of each data point's distance to the mean.

Now let us substitute our given values in above formula.

`\sigma=\sqrt{ ((6-9)^(2)+(5-9)^(2)+(10-9)^(2)+(11-9)^(2)+(13-9)^(2))/(5-1) }`

`\sigma=\sqrt{ ((-3)^(2)+(-4)^(2)+(1)^(2)+(2)^(2)+(4)^(2))/(4) }`

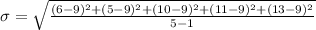
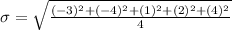
Upon adding the square of distances we will get,

`\sigma=\sqrt{ (9+16+1+4+16)/(4) }`

`\sigma=\sqrt{ (46)/(4) }`

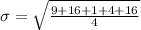
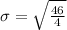
Upon dividing 46 by 4 we will get,

`\sigma=√( 11.5)`

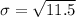
Upon taking square root of 11.5 we will get,

`\sigma=3.3911649915626341\approx 3.39`

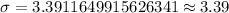
Therefore, the standard deviation for our given data set will be 3.39.