Answer:
The larger angle formed at the intersection of the bike trail and 360th street is 132°
Explanation:
From the diagram, street 350 and street 360 are parallel. The bike trail it the transversal to the parallel streets.
We know that, Alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. And when the two lines being crossed are parallel lines the alternate interior angles are equal.
So
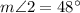
Angle 2 and angle 3 are supplementary angles, so
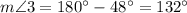
As
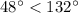 , so the larger angle formed at the intersection of the bike trail and 360th street is 132°.
, so the larger angle formed at the intersection of the bike trail and 360th street is 132°.