Answer:
The probability of drawing exactly two 4, 5, 6, or 7 s is
 .
.
Explanation:
In a standard deck the total number of cards is 52.
There are 4 different suits and each suit have 13 different cards.
13 different cards for one spaed , 13 different card of club, 13 different card of diamond and 13 different card of heart.
So we have 4 card of each number.
The total card of 4,5,6 and 7 s are
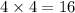
The number of cards which are not 4,5,6 and 7 s,

Use combination to find the probability of drawing exactly two 4, 5, 6, or 7 s.
We have to select 2 card from 16 card, 1 card from another 32 card and 3 card from 52 card.
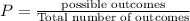
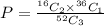
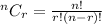
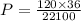
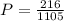
Therefore, the probability of drawing exactly two 4, 5, 6, or 7 s is
 .
.