Question

If the area of the rectangle is 35x^2-53x-18 and its length is 7x+2 inches, find its width

Answer 1

5x - 9

Explanation:

The area of the rectangle is:

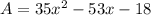`A=35x^2 -53x-18` (1)

The area of the rectangle is the product of length (L) and width (W):

`A=LW`

where
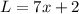`L=7x+2`, and the width must be in the form
`W=ax+b`.

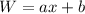We need to find the values of a and b. If we calculate the product of L and W, we get:

`A=LW=(7x+2)(ax+b)=7ax^2 + 7bx+2ax+2b = 7ax^2 +(7b+2a)x+2b`

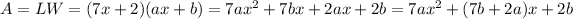
We know that this equation must be equivalent to (1), so we immediately see that:

- the coefficient of the second order term,
`x^2`, must be 35, so

`7a=35\\a=(35)/(7)=5`

- the zero-order term must be equal to -18, so we have

`2b=-18\\b=-(18)/(2)=-9`

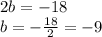
- We can verify that using a=5 and b=-9, the coefficient of the first-order term corresponds to -53:

`7b+2a=7(-9)+2\cdot 5=-63+10=-53`

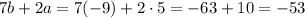
So, the width is

W = 5x - 9