We know that Volume of Cylinder is given by : πr²h
Where : 'r' is the Radius of the Cylinder
'h' is the Height or Depth of the Cylinder
Given : The Height of the Pool is Half of its Radius
⇒ Height of the Pool =
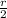
Given : The Volume of the Pool = 1570 feet³
⇒ πr²h = 1570
⇒
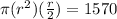
⇒
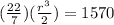
⇒
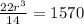
⇒
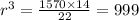
⇒
![r = \sqrt[3]{999} = 10\;(approx)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/k9yrxy23dp2bgu8r56dwbgikkdrlfmlfby.png)
As : Area of the Bottom of the Pool is Circular
We know that Area of Circle is given by : πr²
⇒ Area of the Bottom Floor = π × 10² = 314.15 feet²