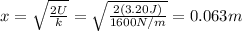Question

A spring of negligible mass has a force constant of 1600 N/m. How far must the spring be compressed for 3.20 J of potential energy to be stored it?

Answer 1

0.063 m

Step-by-step explanation:

The elastic potential energy stored in a spring is given by

`U=(1)/(2)kx^2`

where

k is the spring constant

x is the compression/stretching of the spring

In this problem, we know the energy stored in the spring: U = 3.20 J, and the spring constant: k = 1600 N/m, so we can re-arrange the formula to find the compression:

`x=\sqrt{(2U)/(k)}=\sqrt{(2(3.20 J))/(1600 N/m)}=0.063 m`