Question

The coordinates of the vertices of a rectangle are (−3, 4) , (7, 2) , (6, −3) , and (−4, −1) .

What is the perimeter of the rectangle? Round each step to the nearest tenth.

Enter your answer as a decimal in the box.
[ ] units.

Answer 1

it's 7 unit

Step-by-step explanation: took the test on k12 trust me.

Answer 2

Find out the what is the perimeter of the rectangle .

To prove

As given

The coordinates of the vertices of a rectangle are (−3, 4) , (7, 2) , (6, −3) , and (−4, −1) .

As shown in the graph given below

Name the vertices A (−3, 4) , B(7, 2) , C(6, −3) , and D(−4, −1) .

Formula

`Distance\ formula = \sqrt{(x_(2) - x_(1))^(2) + (y_(2) - y_(1))^(2)}`

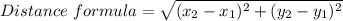
Vertices are A (-3, 4) and B (7,2)

`AB = \sqrt{(7 - (-3))^(2) + (2 - 4)^(2)}`

`AB = \sqrt{(10)^(2) + (-2)^(2)}`

`AB = √(100 + 4)`

`AB = √(104)`

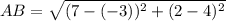
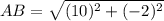
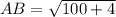
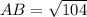
AB = 10.2 units (approx)

As this is the rectangles

Thus AB = CD (The opposite sides of the rectangle are equal.)

CD = 10.2 units (approx)

Now vertices are B(7, 2) and C(6, −3)

`BC = \sqrt{(6 - 7)^(2) + (-3 -2 )^(2)}`

`BC = \sqrt{(-1)^(2) + (-5 )^(2)}`

`BC = √(26)`

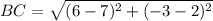
BC = 5.1 units(Approx)

As this is the rectangles

Thus BC = AD (The opposite sides of the rectangle are equal.)

AD = 5.1 units

Formula

Perimeter of a rectangle = 2 (length + Breadth)

As length = 10.2 units

Breadth = 5.1 units

Put in the formula

Perimeter of a rectangle = 2 × (10.2 + 5.1)

= 2 × 15.3

= 30.6 units.

Therefore the perimeter of a rectangle is 30.6 units .