Answer:
65+72i
Explanation:
The given expression is
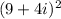
We need to find the simplified form of given expression.
Using perfect square formula, we get
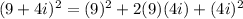
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/e9t794mxoqhryly9cr9k0lu7zpqxrd5ey6.png)
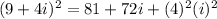
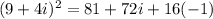
![[\because i^2=-1]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/muljom9yi415qk3cvrpuzv4hoymrrm413r.png)
On further simplification we get
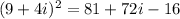
Combined like terms.
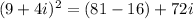
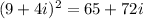
Therefore, the simplified form of given expression is 65+72i.