Question

Write the standard form equation of the ellipse shown in the graph, and identify the foci.

Answer 1

Answer option A

From the given graph is a Vertical ellipse

Center of ellipse = (-2,-3)

Vertices are (-2,3) and (-2,-9)

Co vertices are (-6,-3) and (2,-3)

The distance between center and vertices = 6, so a= 6

The distance between center and covertices = 4 , so b= 4

The general equation of vertical ellipse is

`((x-h)^2)/(b^2) + ((y-k)^2)/(a^2)=1`

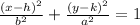
(h,k) is the center

we know center is (-2,-3)

h= -2, k = -3 , a= 6 and b = 4

The standard equation becomes

`((x+2)^2)/(4^2) + ((y+3)^2)/(6^2)=1`

`((x+2)^2)/(16) + ((y+3)^2)/(36)=1`

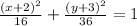
Foci are (h,k+c) and (h,k-c)

`c=√(a^2-b^2)`

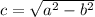
Plug in the a=6 and b=4

`c=√(6^2-4^2)`

`c=√(20)`

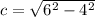
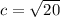
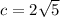`c=2√(5)`, we know h=-2 and k=-3

Foci are
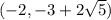`(-2,-3+2√(5))` and
`(-2,-3-2√(5))`

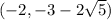
Option A is correct