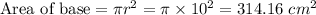Answer:
The area of its bottom floor is 314.16 cm²
Explanation:
Joanne has a cylindrical, with volume as 1570 cm³.
Height of the pool is half of the radius of its base.
Let us assume the length of radius is r cm, so length of its height will be

We know that,
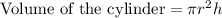
Putting all the values,

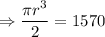
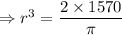
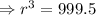
![\Rightarrow r=\sqrt[3]{999.5}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/da186arvmeh1qajyrxjq5aqle9ygwg402z.png)
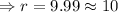
We also know that,