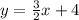I don't know if you have to use a specific form, but I will be using the slope-intercept form, which is:
y = mx + b
"m" is the slope, "b" is the y-intercept (the y value when x = 0)
To find the slope, you can use the slope formula and plug in 2 points. I will use ( -2, 1 ) and ( 0, 4 )
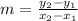
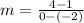
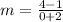
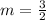
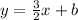
To find "b", you can plug in a point into the equation, or you can look at the table to find the y value when x = 0. When x = 0, the y value is 4, so your y-intercept is 4