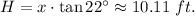Question

The naturalist views an elephant in the distance, but he doesn’t know how far away the elephant is from him. He takes a view to find the a 22 degree angle of elevation. He moves backwards from the elephant pacing off a distance of 27 feet. He takes a second view and determines a new angle of elevation of 11 degrees. How tall is the elephant? How far away was the naturalist when he first saw the elephant

Answer 1

10.11 feet

Explanation:

Let H ft be the elephant's height and x ft be the initial distance from naturalist to the elephant.

1. Naturalist takes a view to find the a 22 degree angle of elevation, then

`\tan 22^(\circ)=(H)/(x).`

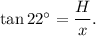
2. Naturalist moves backwards from the elephant pacing off a distance of 27 feet, the distance from naturalist to the elephant becomes (x+27) ft. He takes a second view and determines a new angle of elevation of 11 degrees. Then

`\tan 11^(\circ)=(H)/(x+27).`

3. Solve the system of two equations:

`\left\{\begin{array}{l}\tan 22^(\circ)=(H)/(x)\\\tan 11^(\circ)=(H)/(x+27)\end{array}\right.\Rightarrow (x+27)/(x)=(\tan 22^(\circ))/(\tan 11^(\circ))\approx 2.0785,\\ \\ \\x+27=2.0785x,\\ \\1.0785x=27,\\ \\x\approx 25.0347\ ft.`

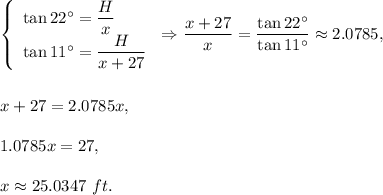
Then

`H=x\cdot \tan 22^(\circ)\approx 10.11\ ft.`