Question

Ali is whirling a 2.0 kg bunch of bananas in a circular path having a radius of 0.50 m. The bananas complete 2 revolutions every 6.0 seconds.

1. What force must he apply to keep the motion constant so that the bananas complete one revolution every 4 seconds?
2. A coin is on a turntable that rotates pi rad/s. The coefficient of static friction between the coin and the turntable is 0.25.
A. Calculation the maximum distance of the coin from the center of the turntable for it to move in a circle.
B. If the coin is placed at a distance of 4.7cm from the center of the turntable, what is the maximum speed of rotation of the turntable for the coin to move relative to the turntable without slipping?

Answer 1

1) 2.467 N

2) a) 0.248m

b) 2.3π rad/sec

Step-by-step explanation:

Given data:

mass of Banana bunch ( m ) = 2.0 kg

radius of circular path ( R ) = 0.5 m

number of revolutions completed = 2

Time to complete 2 revolutions = 6 seconds

1) Determine the force to keep the motion constant for one complete revolution in every 4 seconds

F = mv^2 / r ----- ( 1 )

where V = 2πR/T

where : R = 0.5 , m = 2, T = 4 seconds

Insert values into equation 1

F = 2 * 4π^2 * 0.5/4^2

= 2.467 N

2a) Calculate the maximum distance of coin from center

angular velocity ( w ) = v/r

coefficient of static friction ( μ ) = 0.25

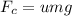`F_(c) = u mg` ---- ( 1 )

mv^2/r = μmg --- ( 2 ) cancelling the mass on both sides eqn 2 becomes

v^2 = μ*g*r

dividing both sides of equation by r^2

w^2 = μ*g/r

hence determine distance ( r ) of coin from center

r = 0.25 * 9.81 / π^2 = 0.248 m

2b ) determine the maximum speed of rotation of the turntable for the coin to move relative to the turntable without slipping

distance coin is placed ( r ) = 4.7 cm = 0.047 m

find speed of rotation ( w )

w^2 = μ*g/r

w = √ 0.25 * 9.81/ 0.047

= 7.2236 rad/secs ≈ 2.3π rad/sec